Common Systems Programming Optimizations and Tricks, Hacker News

Today’s blog post is an overview of some common optimization techniques and neat tricks for doing “systems programming” – whatever that means today. We’ll walk through some methods to make your code run faster, be more efficient, and to squeeze just a little more juice from whatever you got.

All of the examples we’ll go over are also on github at paulcavallaro / systems-programming.

Cache Lines & False Sharing

False sharing is a fairly well-understood problem in optimizing multi-threaded code on modern SMP systems. The problem has beenwrittenaboutFairlyextensively, but the basic idea is that physical memory on a machine isn’t infinitely granular, i.e. you can’t just read a byte. Instead, when you want to read a single byte of memory, the processor will pull in and cache not just that byte, but the surrounding data as well, on the assumption that it will likely be used too. This unit of data that gets read and cached is called a “cache line”, and is essentially the smallest piece of memory that can be accessed.

As of 2019 cache lines are powers of 2, usually in the range of 32 to 256 bytes, with 64 bytes being the most common.

Now, to support multiple processors on a single machine reading and writing from the same memory in a coherent way, only one processor on a machine can have exclusive access to a given cache line.

False sharingis when you accidentally put two unrelated pieces of data in the same cache line. Now having two processors update separate chunks of data, say counters, will interfere with one another, as each processor attempts to gain exclusive access to the cache line that houses both fields.

The explanation for the namefalse sharingis that even though these two counters shouldn’t be affecting one another from a correctness standpoint, they are – big air quotes incoming – “falsely sharing” a cache line for no good reason.

One solution is to force the data onto separate cache lines, which you can do in C / C by forcing the alignment of the members of a struct / class. Inexamples / cache-lines.ccwe use absl’sABSL_CACHELINE_ALIGNEDmacro to achieve this.

To show the effect in practice, we benchmark two different structs ofstd :: atomiccounters,NormalCountersandCacheLineAwareCounters.

// NormalCounters is straight forward naive implementation of a struct of// counters.// Note: We also use ABSL_CACHELINE_ALIGNED on the NormalCounters struct, but// not its members, so that the entire struct will be aligned to a cache line.// Otherwise the struct might be placed towards the end of a cache line,// accidentally straddling two cache lines, thereby improving its performance.structABSL_CACHELINE_ALIGNEDNormalCounters{  STD::atomicint 64>success{(0)};  STD::atomicint 64>failure{(0)};  STD::atomicint 64>okay{(0)};  STD::atomicint 64>(meh) ************************{(0)};};// CacheLineAwareCounters forces each counter onto a separate cache line to// avoid any false sharing between the counters.// Note: We must use ABSL_CACHELINE_ALIGNED for each member, since we want to// pad every single counter so it will be forced onto its own separate cache// line.structABSL_CACHELINE_ALIGNEDCacheLineAwareCounters{  ABSL_CACHELINE_ALIGNEDSTD::atomicint 64>success{(0)};  ABSL_CACHELINE_ALIGNEDSTD::atomicint 64>failure{(0)};  ABSL_CACHELINE_ALIGNEDSTD::atomicint 64>okay{(0)};  ABSL_CACHELINE_ALIGNEDSTD::atomicint 64>(meh){(0)};};

The benchmark uses either 1, 2, 3, or 4 threads, each bumping a separate atomic counter inside the struct 64 K times. Here are the results on a 2013 MacBook Pro with a Haswell processor:

Executingtestsfrom//examples: cache-lines------------------------- -------------------------------------------------- -CacheLineSize:64Sizeof(NormalCounters)=64Sizeof(CacheLineAwareCounters)=2562019-08-1301:16:18Runon(4X2800(MHz)CPUs)CPUCaches:  L1Data32(K) ************************((x2))  L1Instruction32(K) ************************((x2))  L2Unified262K(x2)  L3Unified4194K(x1)------------------------- --------------------------------------------------BenchmarkTimeCPUIterations------------------------- --------------------------------------------------BM_NormalCounters/threads: 1389US387US1812BM_NormalCounters/threads: 21264US2517US234BM_NormalCounters/threads: 31286US3718US225BM_NormalCounters/threads: 41073US3660US204BM_CacheLineAwareCounters/threads: 1386US385US1799BM_CacheLineAwareCounters/threads: 2200US400US1658BM_CacheLineAwareCounters/threads: 3208US581US1152BM_CacheLineAwareCounters/threads: 4193US721US1008

A note on these results:Timemeasures wall clock time per-thread andCPUmeasures cpu time per-thread.

We can see that the sizes of the two structs are different, wheresizeof (NormalCounters)=64andsizeof (CacheLineAwareCounters)=256. This is because the alignment constraint we put on the individual fields, such that each member is on its own cache line. So instead of anint 64taking up 8 bytes like usual, it’s taking up a full cache line, which is 64 bytes on my machine.

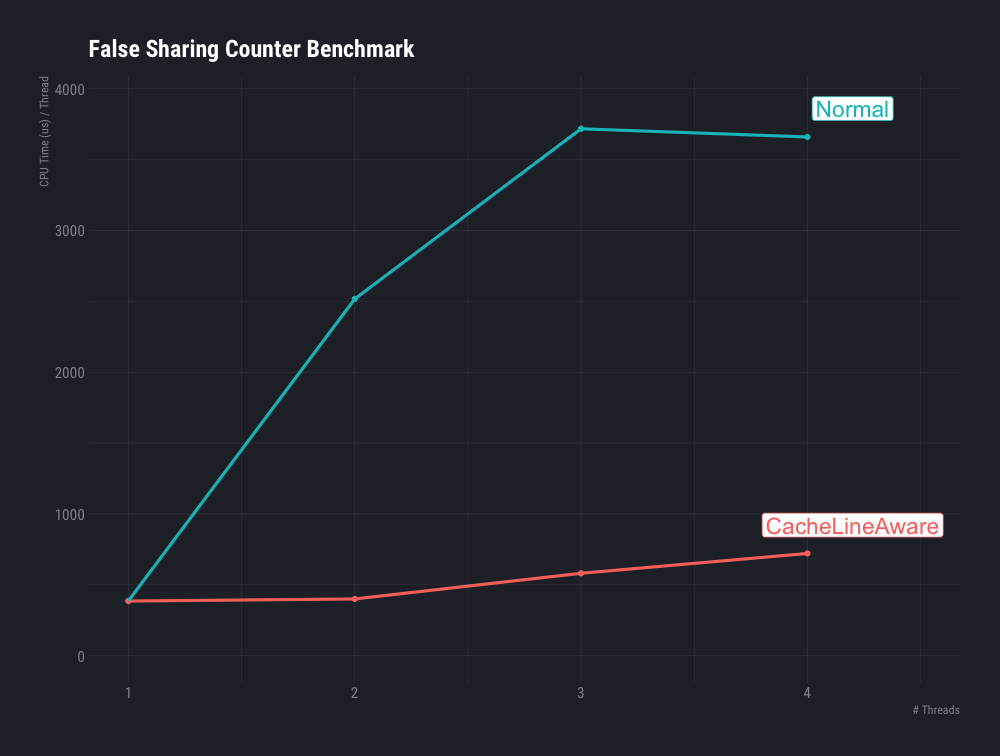
We also see that for the single threaded case, theNormalCountersvs.CacheLineAwareCountersperform indistinguishably. But as we add more threads, theCacheLineAwareCountersperform much better than the naive normal counters that suffer from the false sharing.

Interestingly the wall clock time spent forCacheLineAwareCountersis higher for one thread than multiple threads, which could point to perhaps some subtle benchmarking problem, or maybe a fixed amount of delay that’s getting attributed across more threads now, and so is smaller per-thread.

The Magic Power of 2: Division Is Slowaloo

In current hardware, division is one of the most expensive operations, where expensive here means “longest latency ”.Agner Fog’s listing of instruction latencieslists Intel Skylake’sDIVinstruction operating on two 64 bit registers having a latency of 35 – 88 cycles, compared to anADDinstruction operating on the same two 64 bit registers having a latency of 1 cycle. So it would behoove us to avoid division where some other set of operations would work.

One place where division is commonly used besides for actually doing division, is in the modulo%operator. And a common place for the modulo operator is in hash tables: to go from a hash to a bucket we computeHASH% TABLE_SIZE. Modulo is used even more heavily inopen-addressingschemes since we’re constantly remapping values ​​back into the hash table bucket space.

So how do we go from using modulo to something else? Bit twiddling and the Magic Power of 2!

First, let me give away the answer: We’re going to force all of our hash tables to be a size that’s a power of 2.

We’ll be able to take advantage of this property for replacing division with faster bit twiddling. Also, this property is easy to maintain since we double the size of our hash table whenever we grow to amoritize the cost of rehashing, so the size will stay a power of 2 as we grow.

Now, we were using division – or modulo – for the purpose of mapping any hash value to a bucket index in our hash table. Bucket indices must be strictly less than our size, and this mapping should not lose any entropy from the hash value.

Instead of using division to do this, we’ll use a bitmask that will “mask” away all set bits except those that are strictly less than our power of 2. This way we keep all the entropy in the least significant bits, just like modulo, but it’s much faster – Agner Fog lists it at 1 cycle latency on the same Intel Skylake architecture.

As a quick refresher on bit twiddling and to explain how we’ll choose our bitmask, let’s look at some bit patterns.

Since numbers are represented in binary, we know that every power of 2 numberNonly has one bit set. For example:

Decimal|Binary    2|00000010    8|00001000   32|00100000  128|10000000

And that means allN - 1‘s have every less significant bit thanlog2 (N)set. For example:

Decimal|Binary    1|00000001    7|00000111   31|00011111  127|01111111

So in order to replace our modulo operator in theHASH% Ncalculation, we instead calculateHASH & (N - 1)using bitwise AND. This will only keep the set bits that are less significant than ourlog_2 (N)bit, mapping anyHASHvalue onto a number in the interval[0, N). We can even cache this bitmask if we want so we don’t have torecompute it in the future.

To show how much faster this bitmask trick is than using normal modulo operator,I’ve written asmall benchmarkto measure executing 1M modulo operations, versus executing 1M bitmasks.

Executingtestsfrom//examples:power-of-two-----------------------------------------------------------------------------2019-08-1302:24:03Runon(4X2800MHzCPUs)CPUCaches:L1Data32K(x2)L1Instruction32K(x2)L2Unified262K(x2)L3Unified4194K(x1)--------------------------------------------------------Benchmark             Time       CPUIterations--------------------------------------------------------BM_Mod             9261us   9234us     75BM_BitMask          325us    324us   1984

Here we can see how theDIVinstruction used by the modulo operator is on theorder of 28x slower, near the 35x slow down predicted by Agner Fog’s latencynumbers.

Since this trick is easy to do, and provides a nice win, it’s used by manyhigh-performance hash-tables, like absl’s “Swiss Tables”flat_hash_set and flat_hash_mapandConcurrencyKit’s ck_ht_map.

Repurposing Top Bits

Oftentimes you want to store a bit or two of extra information along with apointer – in fact it’s so commonWikipedia has an article about it. Oneway to do this is to take advantage that on many 64-bit systems, such as linux,virtual memory addresses are only 48 bits wide, even though we use 8 bytes tostore them.

This means, we can just store any old crap we want to in the top 16 bits by justmasking it out whenever we want to actually dereference it. Here’s someexample C codeof using the top bit of a pointer to store whether the underlying data is“dirty” or not.

constexpruintptr_tkDirtyBit=0x8000000000000000;constexpruintptr_tkPtrMask=0x7fffffffffffffff;static_assert(sizeof(uintptr_t)==8,"Only works on 64-bit systems");templatetypenameT>uintptr_tMarkDirty(T*t){returnreinterpret_castuintptr_t>(t)|kDirtyBit;}templatetypenameT>T*GetPointer(uintptr_tt){returnreinterpret_castT*>(t&kPtrMask);}

Interestingly though, since this is a feature of Linux’s memorymanagement/virtual address space, it is subject to change – and it actuallyhas!

LWNreported on the patchset in 2017implementing five-level page tables in order to support larger amounts ofaddressable memory. The change, if enabled, would move Linux from 48-bit virtualaddresses to 57-bit virtual addresses, increasing virtual address space from 256TiB to 128 PiB – which ought to be enough for everyone 😀.

Part of why the change couldn’t be enabled by default is because various highperformance programs, notably various JavaScript engines andLuaJIT, use this repurposing trick to pack some extra datainto pointers.

Lock Striping

Locks can be used for mutual exclusion when you want to have multiple threadsaccess shared data exclusively. The downside though is if the shared data isfrequently accessed and the critical section is non-trivial, your threads couldspend most of their time contending on the lock, instead of actually doing work.

One common way of solving this problem, is introducing more locks. Wait – what?

Well, instead of one lock that guards all of the data, instead you have manylocks responsible for just a piece of the data. In this way we shard the datainto separate independent buckets that don’t contend with each other. Assumingthe data access is uniform-ish, increasing sharding of the data reduces thenumber of threads contending on a lock proportionally.

Below is asmall C exampleof two implementations of thread-safe hash set. The first implementation,ThreadSafeHashSet, just uses a single lock to guard a single underlyingabsl::flat_hash_set. The second implementationLockStripedHashSethasNseparate locks, guardingNseparateabs::flat_hash_sets.

// Simple thread-safe single-lock hash setclassThreadSafeHashSet{public:voidInsert(uint64i){ absl::MutexLocklock(&mu_); hash_set_.insert(i);}boolContains(uint64i){ absl::MutexLocklock(&mu_); returnhash_set_.contains(i);}private:absl::Mutexmu_;absl::flat_hash_setuint64>hash_set_;};// Chunk the data into `kNumChunks` separate hash sets, guarded by separate// locks.templatesize_tkNumChunks>classLockStripedHashSet{public:voidInsert(uint64i){ // Mod the data to calculate which hash_set/lock to useconstsize_tidx=i%kNumChunks; absl::MutexLocklock(&mu_[idx]);    hash_set _[idx].insert(i);  }  boolContains(uint 64(i)){    constsize_tidx=i%kNumChunks;    ABSL::MutexLocklock(&mu _[idx]);    returnhash_set _[idx].contains(i);  } private:  STD::arrayABSL::Mutex,kNumChunks>mu _;  STD::arrayABSL::flat_hash_setuint 64>,kNumChunks>hash_set _;};

To illustrate the benefits of lock striping, we benchmark the performance of the two thread-safe hash sets in the presence of many threads, each inserting 1M items. For theLockStripedHashSetwe try with 4 chunks and with 8 chunks. The results are below:

Executingtestsfrom//examples: lock-striping------------------------- -------------------------------------------------- -2019-08-2422:24:37Runon(4X2800(MHz)CPUs)CPUCaches:  L1Data32(K) ************************((x2))  L1Instruction32(K) ************************((x2))  L2Unified262K(x2)  L3Unified4194K(x1)------------------------- -------------------------------------------------BenchmarkTimeCPUIterations------------------------- -------------------------------------------------BM_SingleLock/threads: 165(ms)65ms11BM_SingleLock/threads: 2ms254ms2BM_SingleLock/threads: 3msms3BM_SingleLock/threads: 4142(ms)405ms(4)BM_LockStriping_4_Chunks/threads: 171ms69ms(9)BM_LockStriping_4_Chunks/threads: 290ms178(ms)   (4)BM_LockStriping_4_Chunks/threads: 389ms248ms3) ************************BM_LockStriping_4_Chunks/threads: 482ms299ms4BM_LockStriping_8_Chunks/threads: 170(ms)69ms10BM_LockStriping_8_Chunks/threads: 274ms143ms4BM_LockStriping_8_Chunks/threads: 371ms198ms(3)BM_LockStriping_8_Chunks/threads: 460(ms)200ms4

Again,Timemeasures wall clock time per-thread andCPUmeasures cpu time per-thread. Also note that since my machine only has 4 logical cores, this test only goes up to 4 threads, since anything beyond that doesn’t actually introduce any extra contention.

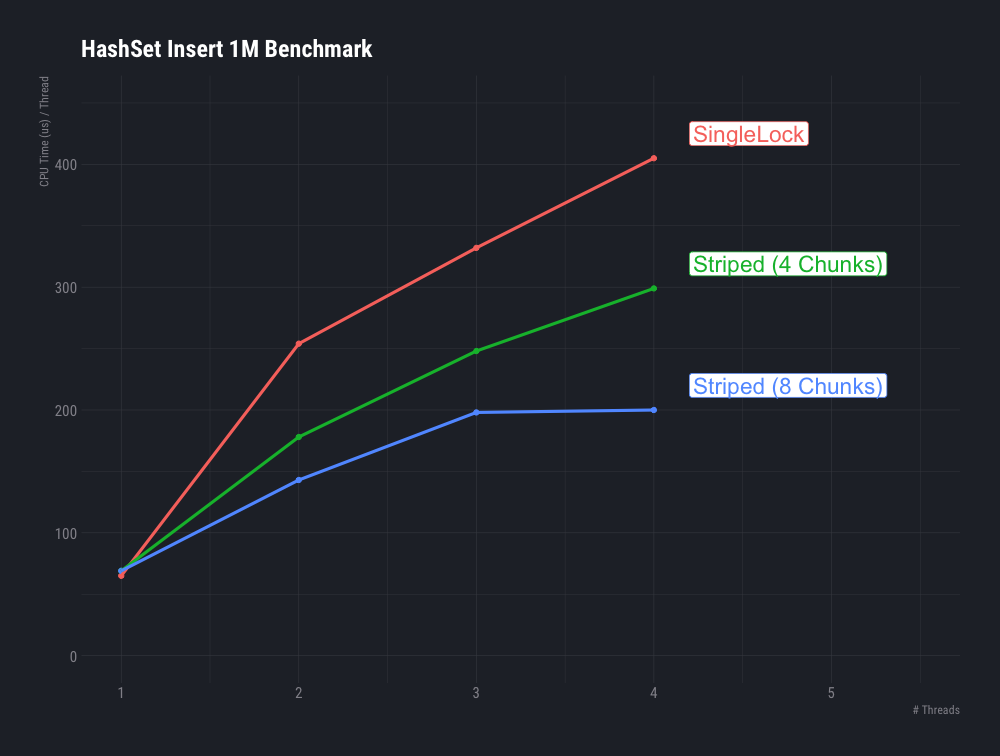
We can see that in the single-threaded case theLockStripedHashSet, no matter the chunking, performs slightly worse on both wall clock and CPU time than the simpleThreadSafeHashSet.

However, as more threads are added, increasing the contention on the locks, theLockStripedHashSetperforms much better, and the 8 chunk version outperforms the 4 chunk version at higher thread counts.

While lock-striping can help alleviate contention on locks, it does have the downside of increasing storage overhead for the locks. In our example the overhead of 7 extra locks and extraabsl :: flat_hash_setbookkeeping is miniscule for a single instance in our benchmark, but if you replaced all the hash sets in an application with an 8-way striped thread-safe hash set, you could bloat its memory footprint by a significant amount.

Conclusion

While this is nowhere near an exhaustive list of the most common systems programming tricks, hopefully it whets your appetite to learn more, provides some tools for improving performance in your own applications, or at least make it easier to understand why performance sensitive code is doing what it’s doing.

Thanks to Mason Simon and Ray Yang for reviewing drafts of this post.