Overview
There are two basic data structures: array and list. Array is a random access data structure but with an expensive line-time insert / erase operation. On the contrary, list is a sequential access data structure but it has fast constant-time insert / erase operation. In this paper I’ll describe a random access data structure named modestly IgushArray which like an array has fast constant-time access operation, but insert / erase operation takes only O (N ^ 1/2) time. The structure can be considered as “fast array” or “array with fast insert operation”. Comparison to other structures can be seen in the table below.
| Array | IgushArray | List | |
|---|---|---|---|
| Access | O 1) | O 1) | O N) |
| Insert | O N) | *********************************************** (O) N^1/2) | O 1) |
| Erase | O N) | *********************************************** (O) N^1/2) | O 1) |
| O 1) * | O 1) * | O 1) | |
| O N) | *********************************************** (O) N^1/2) | O 1) |
Motivation
Motivation was the need for an array which can be kept sorted and one could quickly access k-th max element and at the same time quickly insert or delete an element.
Implementations
-
This implementation written in C .Array class fully implements std :: vector interface, so it is very easy to replace std :: vector in code;
-
C # – (cser / IgushArray) ;
Structure
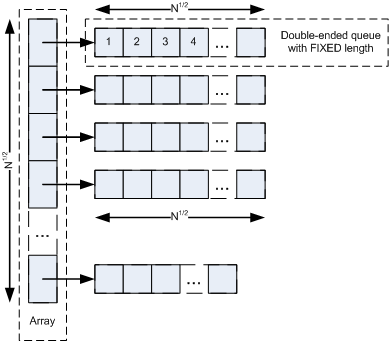
IgushArray is an array of pointers withapproximatesize of N ^ 1/2 and each element points to a double-ended queue withapproximatesize of N ^ 1/2.All DEQs have the same sizeexcept last one (last one can have less than N ^ 1/2 size). See picture below.
The size of the array can be changed during work with the structure; the size of DEQs isneverchanged. But after some work with a structure it can be done total reconstruction to adjust array and DEQs size to approximately N ^ 1/2.It is also highly recommended to know the approximate size of a future structure during creation to initially calculate optimal sizes. Otherwise the size of DEQ would 1 and insert / erase time would degenerate to linear.
A DEQ can be implemented using array (set of arrays) or list. In first case it provides constant-time access, but linear-time insert / erase, in second case it provides linear-time access, but constant-time insert / erase. It is very important that in IgushArray s DEQ should be implemented using first approach. Also in IgushArray the size of DEQs is know during creation and never changed, so this fact can be used and a DEQ can be implemented usingonly one arraywhich would improve and simplify the implementation.
So, array and DEQ, used in IgushArray implementation, itself are random access data structures.
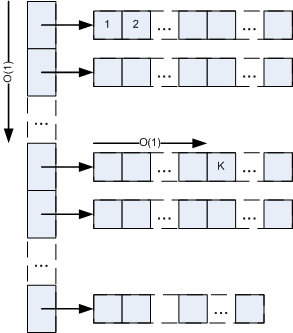
Access
To access a random element by its index in Igush is needed to calculate index in pointers array by (K / deq_size) operation (O (1) ), than obtain the pointer (O (1)), calculate index in DEQ byK% deq_sizeoperation (O (1)) and obtain the element in DEQ. See picture below. It can be seen, that access operation has constant-time complexity.
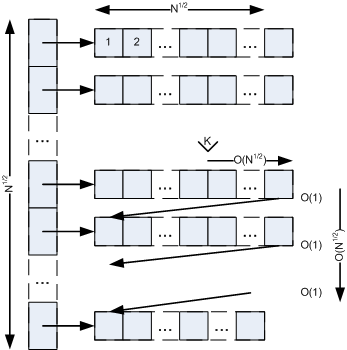
Insertion
To insert a new element into IgushArray, it is needed to insert the element into particular position in particular DEQ (O (N ^ 1/2)) and “Move” the elements in this and the next DEQs down. “Moving” element down means that it’s needed to pop an element from the end of a DEQ and push it to the beginning to the next one. Each moving has O (1) complexity. It is needed to “move” down less than N ^ 1/2 elements (O (N ^ 1/2)). See picture below. It can be seen, that total operation has O (N ^ 1/2) complexity.
An insertion may require a push back to the end of the pointers array and creation of a new DEQ (in case of the last DEQ is full). The operation may take O (N ^ 1/2) time and wouldn’t damage total performance.
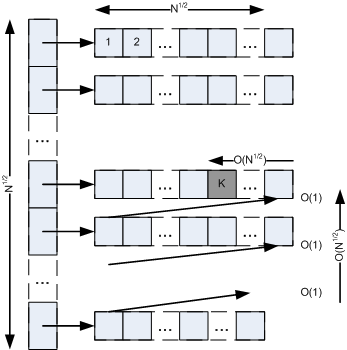
Erasing
To erase an element in IgushArray, it is needed to erase the element in particular DEQ (O (N ^ 1/2)) and “move” the elements in this and the next DEQs up. “Moving” element up means that it’s needed to pop an element from the beginning of a DEQ and push it to the end to the previous one. Each moving has O (1) complexity. It is needed to “move” up less than N ^ 1/2 elements (O (N ^ 1/2)). See picture below. It can be seen, that total operation has O (N ^ 1/2) complexity.
An erasing can require a destruction of last DEQ (in case of the last DEQ has one element).
Generalization
It can be noticed that array which is used in DEQ implementation can be IgushArray by itself and so on. In this case the complexity of access operation would be O (k) where k is degree; the complexity of insert / erase operation would be O (N1 / k). In simple case described in this paper k is 2.
The package performance test results can be seen below. The tests were done using computer with next configuration: Inter Core 2 Duo 1, 83 MHz, 2GB, Ubuntu, GCC version 4.5.2. The results are in milliseconds. Every operation was performed 1000 times.
Below there are the results of calculating the sum of a structure .
| Count | IgushArray | std :: vector | Result |
|---|---|---|---|
| Slower: 8 | |||
| 10 000 | Slower: 7.6 | ||
| 100 000 | Slower: 7.3 | ||
| Slower: 5.7 | |||
| 10 000 000 | Slower: 6.9 |
It can be seen that the time of sum grows linear as count of elements. It means that the both structures have constant-time access operation.
Access by Iterator
Below there are the results of calculating the sum of a structure .
| Count | IgushArray | std :: vector | Result |
|---|---|---|---|
| Slower: 4.2 | |||
| 10 000 | Slower: 5 | ||
| 100 000 | Slower: 4.9 | ||
| Slower: 4.9 | |||
| 10 000 000 | Slower: 4.9 |
It can be seen that the time of sum grows linear as the count of elements.
The worse access time of IgushArray is due to IgushArray generally is more complicated structure than array.
Below there are results of inserting one element in the middle.
| Count | IgushArray | std :: vector | Result |
|---|---|---|---|
| Same time | |||
| 10 000 | Faster: 3 | ||
| 100 000 | Faster: 6 | ||
| Faster: 45 | |||
| 10 000 000 | Faster: 67 |
It can be seen that the time of std :: vector insert operation grows linear as the count of elements, but the time of IgushArray insert operation grows like N ^ 1/2.
Erasing
Below there are results of erasing one element from the middle.
| Count | IgushArray | std :: vector | Result |
|---|---|---|---|
| Same time | |||
| 10 000 | Slower: 4 | ||
| 100 000 | Faster: 5 | ||
| Faster: 16 | |||
| 10 000 000 | Faster: 53 |
It can be seen that the time of std :: vector erase operation grows linear as the count of elements, but the time of IgushArray erase operation grows like N ^ 1/2.
This implementation written in C .Array class fully implements std :: vector interface, so it is very easy to replace std :: vector in code.
It is highly recommended to know the approximate size of a future structure and transfer it to the constructor or immediately after creation to reserve () function to initially calculate optimal sizes. Otherwise, the size of DEQ would 1 and insert / erase time would degenerate to linear.
The implementation also provides FixedDeque class. The class is a simple double-ended queue which uses only one array in its implementation and requires its size during creation (in constructor). It does not fully implements std :: deque interface and provides only functions needed by IgushArray implementation.
Limitations
Regardless of the IgushArray class implements std :: vector class, there are cases when std :: vector is used as a buffer. In these cases, std :: vector cannot be replaced, because in Igush are not stored sequentially in memory. Also in these cases insert and erase time is not an issue.
IgushArray class fully provides iterator mechanism, but this mechanism does not guarantee an iterator consistence after modifying operations such as insert / erase, push back / pop back and so on.
Test Packs
The package has also two stability test packs and performance test pack . Stability test pack tests almost all IgushArray interface functions and compares results it with std :: vector as a baseline. There is same pack for FixedDeque.
Performance test pack compares the results of main Igush (access, insert / erase) performance with std :: vector performance. Main dependences can be seen using this pack (see below).
Port to Other Languages
- C # –cser / IgushArray






GIPHY App Key not set. Please check settings