Noether's Theorem – A Quick Explanation, Hacker News

) Noether’s Theorem issuper rad. The theorem is, colloquially,

>>Continuous symmetries imply conserved quantities.(Let’s dig into the origin of this powerful theorem and list a couple of examples. I’ll restrict my attention to a subclass of symmetries for the sake of space, buuuut if there’s interest, I could do a more general post in the future. (Heads up:because this post is written using LaTeX, it’s probably easiest to read directly from my blog.) •  Defining the Lingo:ALagrangianis a function that (after some manipulation) yields the physical evolution of a system. A generic Lagrangian $ L $ can be a real continuous function of …******************** ($ m $ realparameters$ t_j $, where $ j=1, cdots, m $, and $ n $ pairs of
paths, which we label $ q_i (t_1, cdots, t_m) $ and $ tilde {q} _i (t_1, cdots, t_m) $, where $ i=1, cdots, n $ and a path means “a real continuous function of the aforementioned parameters”

In this exceedingly general case, we might write

$$ L=L (q_1, cdots, q_n, tilde {q} _1, cdots, tilde {q} _n, t_1, cdots, t_m) $$

However

, for the sake of clarity, let’s restrict ourselves to one parameter $ t $ and one function pair $ (q, tilde {q}) $. Let’s further suppose $ L $ depends on its parameter only through the function pair, aka let us write $ L=L (q, tilde {q}) $ (as opposed to $ L=L (q, tilde {q} , t) $). This is the case relevant to a classical particle confined to a friction-free line, wherein $ q (t) $ is the particle’spositionalong the line and $ t $ records thetime (*****************.

While $ L $ is constructed to be. a function of position $ q (t) $ and some other path $ tilde {q} (t) $, we always intend to eventually set $ tilde {q} (t) $ equal to the velocity $ dot {q} equiv dq / dt $. Furthermore, of the many combinations $ (q (t), tilde {q} (t)) $ equaling $ (q (t), dot {q} (t)) $, nature chooses the pair satisfying the (Euler-Lagrange equation:)

$$ left. frac { partial L} { partial q} right | _ {{ tilde {q}= dot {q}}  = frac {dp} {dt} $$

where

$$ p equiv left. frac { partial L} { partial tilde {q}} right | _ {{tilde {q}= dot {q}} $$

The differential equation we get from plugging a specific $ L $ into the Euler-Lagrange equation is called the
equation of motionof the system, and $ p $ is themomentum conjugate to $ q $.

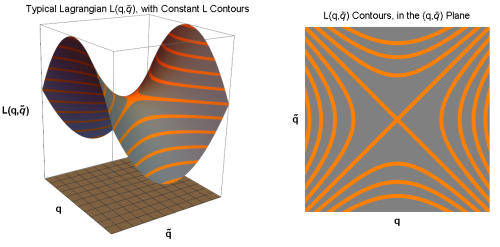
•   The Main Idea:No matter the specific form of $ L $, we can plot it over $ (q, tilde {q}) $ space. (To be clear: this is the space of values ​​to which the paths $ q (t) $ and $ tilde {q} (t) $ are mapping, so essentially the real plane.) The resulting plot will look something like the left plot in the following image:

*********************** I’ve made a point to highlight contours of constant $ L $ in orange. The right plot projects those contours onto the $ (q, tilde {q}) $ plane. These contours lie at the heart of Noether’s Theorem: imagine we slide the coordinates $ (q, tilde {q}) $ around in the plane so that each point moves continuously along a contour of constant $ L $. Usually the shape of $ L $ is changed when we distort the $ (q, tilde {q}) $ plane below it, but by forcing each $ (q, tilde {q}) $ to flow along a contour, $ L $ is unaffected! A continuous transformation that leaves $ L $ unchanged is called acontinuous symmetryof the Lagrangian.We can make this whole business quantitative by parameterizing the sliding operation with a real variable $ alpha $. Let’s choose $ alpha $ so that $ alpha=0 $ corresponds our initial unchanged $ (q, tilde {q}) $ plane. Then the statement “$ alpha $ parameterizes contours of constant $ L $” is mathematically expressible as

$$ left. frac {dL} {d alpha} right | _ { alpha=0}=0 $$

which equals, by the chain rule of differentiation,

$$ frac { partial L} { partial q} hspace {3 pt} left. Frac {dq} {d alpha} right | _ { alpha=0} frac { partial L} { partial tilde {q}} hspace {3 pt} left. frac {d tilde {q}} {d alpha} right | _ { alpha=0}=0 $$

Now, this equation holds true acrossallof $ (q, tilde {q} ) $ space, including along the physical path solving the equations of motion. For that path, we may use the Euler-Lagrange equation, the definition of conjugate momentum $ p equiv partial L / partial tilde {q} $, and the fact that $ partial dot {q} / partial alpha=d / dt ( partial q / partial alpha) $ to write,

$$ frac { dp} {dt} hspace {3 pt} frac { partial q} { partial alpha} p hspace {3 pt} frac {d} {dt} left [frac{partial q}{partial alpha}right]=0 $$

aka, according to the product rule of differentiation,

$$ frac {d} {dt} left [phspace{3 pt}frac{partial q}{partial alpha}right]=0 $$

In other words, the value of $ p hspace {3 pt} ( partial q / partial alpha) $ doesn’t change in time – it’s aconserved quantity!This is a special case of Noether’s Theorem.

If we repeat the above calculation with $ n $ paths $ q_i (t) $, we instead derive

$$ text {*} hspace { pt} frac {d} {dt} left [vec{p}cdot frac{dvec{q}}{dalpha}right]=0 hspace { pt} text {*} $$

where $ vec {q} equiv (q_1, cdots, q_n) $ and $ vec {p} equiv (p_1, cdots, p_n) $, and we find that

>>Momentum along a continuous symmetry direction is conserved.

This powerful statement allows us to identify conserved quantities from symmetries alone. For example …

•   1. Coordinate Translation Symmetry:Suppose $ L $ doesn’t depend on the coordinate $ q_i $ for some value of $ i $. Then the translation $ q_i mapsto q_i alpha $ is a continuous symmetry transformation. Because $ dq_k / d alpha $ is nonzero only for the coordinate we’re transforming ($ k=i $), the associated conserved quantity is…

$$ vec {p} cdot frac {d vec {q}} {d alpha}=p_i $$

which is the $ i $ th conjugate momentum. And so,coordinate translation invariance necessarily implies conservation of the corresponding momentum.

(****************** •    2. Rotational Symmetry:Suppose $ L $ depends on the coordinates $ (x, y, z) $ and is invariant under the rotation of $ x $ and $ y $ into one-another:

$$ x mapsto ( cos alpha) x ( sin alpha) y hspace { pt} y mapsto ( cos alpha) y – ( sin alpha) x $$

Then we may calculate, $$ left. frac {dx} {d alpha} right | _ { alpha=0}=y hspace {50 pt} left. frac {dy} {d alpha} right | _ { alpha=0}=-x $$

from which Noether’s Theorem implies conservation of…

$$ vec {p} cdot frac {d vec {q}} {dt}=p_x y – p_y x=- L_z $$

where $ L_z $ is the angular momentum in the $ z $ -direction.Rotational invariance necessarily implies angular momentum conservation.

•   Closing Comment:Note how we didn’t need an explicit form for $ L $ to make these arguments. Noether’s Theorem tells us that conserved quantities naturally emerge not as coincidences, but from the presence of symmetries. Consequently, if I experimentally observe a conserved quantity (like electric charge, or color charge, or even things like lepton number) then I can make my model consistent with that observation by encoding certain symmetries into my Lagrangian. In this way, Noether’s Theorem is impressive in both its elegance and practical power.

Thanks for the ask, anonymous! I hope this helped. Although I did not have space to discuss it here, Noether’s Theorem also extends to Lagrangians with explicit parameter dependence, systems with multiple evolution parameters (like QFT), instances where $ (q, tilde {q}) $ transformations change $ L $ by a total derivative, and more. One extension allows us to demonstrate how time translation invariance yields energy conservation.

) Have a physics question you think I might be able to help answer? Send me an ask. Until then, have a great day! Best wishes, my friend!

************************ () ****************************************